E8 - Skip Garibaldi

You may have heard some of the news stories about E₈, such as:

E₈ provides the densest sphere packing in 8 dimensions (media, arxiv).
Experimental physicists reported detecting “emergent E₈ symmetry” in the laboratory, corroborating predictions made 20 years earlier by Zamolodchikov and others. The experiment is fascinating on its own, even ignoring the connection with E₈. For an exposition of this aimed at mathematicians, see my paper with David Borthwick.
The “calculation the size of Manhattan” was widely reported in the news media in 2007. This was the result of some serious mathematical effort by the Atlas of Lie groups project. They calculated the Kazhdan-Lusztig-Vogan polynomials for the split real E₈. David Vogan described it for mathematicians in this paper.
The “Exceptionally Simple Theory of Everything” claimed to unify the four fundamental forces of physics using a real form of E₈. This turned out to be no more scientific than cold fusion; see my paper with Jacques Distler for a disproof. It was described in an article in Ars Technica.

E₈ is also mentioned as playing a role in the fictional Beard-Einstein Conflation in the novel Solar by Ian McEwan.

But what does “E₈” mean?

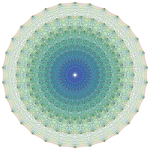
It can be:

a root system. This is a collection of 240 points in 8-dimensional space. The graphic you see here shows a projection of it into a well-chosen plane.
a lattice in 8-dimensional space.
a complex Lie group. The Wikipedia entry on E₈ gives an introduction to this and the two items below.
one of three different real Lie groups whose complexification is the complex Lie group E₈.
an algebraic group over a field related to the complex Lie group

There have been exciting recent developments in this century about E₈ also in pure mathematics, especially related to cohomological invariants.

The torsion index of E₈ was calculated to be 2880 by Burt Totaro in two papers.
The essential dimension of E₈, a single number that aims to measure how complicated the group is, has been known to be between 9 and 231 since 2000. That’s a wide range! In 2024 it was shown to be at least 56 (link).
The Rost invariant (degree 3) modulo 5 has an explicit formula determined by Philippe Gille and Anne Quéguiner-Mathieu.
The kernel of the Rost invariant (degree 3) modulo 3 is known by Vladimir Chernousov, and this has been reproved using Chow motives by myself, Victor Petrov, and Nikita Semenov.
Serre’s Conjecture II was proved for function fields of complex surfaces by de Jong, He, and Starr.
The Kneser-Tits Conjecture was settled for one of the two rank-2 forms of E₈ by Parimala, Jean-Pierre Tignol, and Richard Weiss.
Bob Guralnick and I showed that E₈ can be viewed as the stabilizer of a degree 8 homogeneous polynomial on a 248-dimensional vector space, or the automorphism group of a commutative nonassociative 3875-dimensional algebra. Later, Maurice Chayet and I explicitly described the multiplication on this algebra and it was described as a decomposition algebra by De Medts and Van Couwenberghe.

For a more detailed and technical discussion of these subjects, see the survey in Bulletin of the AMS.

Here are some things that should have appeared in the survey article but didn’t:

A question: For the fundamental Weyl modules of E₈, it is known for which characteristics they are irreducible. In the cases where they are reducible, the composition factors do not seem to be known, even down to specific questions such as whether the trivial module occurs in the head of the radical.
A reference: The end of the paper “Finite H-spaces and Lie groups” by J.F. Adams contains a “Letter from E₈“. Recommended reading!