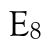A generic stabilizer

Back in the 1970s and 1980s, a bunch of people proved a host of results about finite-dimensional irreducible representations of simple Lie algebras over the complex numbers. They discovered a startling dichotomy: in various ways, small representations behave similarly to each other and large representations behave similarly to each other. Moreover, the difference between “small” and “large”, while the precise value depends on the algebra under consideration, is quite close to the dimension of the algebra.

Proving analogous results over fields of prime characteristic presents serious difficulties. For example, general techniques in characteristic zero prove the existence of a stabilizer in general position (i.e., an open set of vectors whose stabilizers are all conjugate), but this technique does not work in prime characteristic. A first step in transferring the bulk of the results to prime characteristic appears to be determining the generic stabilizer in each case. Moreover, determining the generic stabilizer has various other applications, such as to essential dimension.

In a series of papers with Bob Guralnick (part I, II, III and our earlier paper on spin groups) we settle this on the level of Lie algebras. Combined with a long work of Guralnick, Lawther, and Liebeck that determines the generic stabilizer on the level of groups of points, this determines the generic stabilizer as a group scheme.

I am ecstatic to be releasing these papers, as they have been a long time in the making. My part of this began shortly after I started work at IPAM at UCLA, back in fall of 2013.